Design space exploration

This post provides a visual guide to design space exploration and its connection to optimisation and uncertainty quantification.

Explore the repo: design-space-exploration

Motivation

Efforts at the intersection of machine learning and simulation generally fall into two main categories: (1) accelerating simulations and (2) enhancing design space exploration and optimisation. These categories are interconnected, forming a feedback loop where advances in one area can significantly impact the other. Accelerating simulations can unlock outer-loop applications that are currently infeasible due to the high computational cost associated with numerous repeated simulations. Conversely, improving design space exploration can drastically reduce the number of simulations needed to identify optimal designs or strategically navigate the design space to minimise uncertainty. This post provides a visual guide to design space exploration, aiming to build intuition without relying on formal mathematics.

Design space

The design space is a multidimensional representation of all possible design configurations, with each point representing a unique combination of design parameters and their associated performance. The following contour plot illustrates the relationship between two design parameters, $X_1$ and $X_2$, and the corresponding values of the objective function. In many engineering applications, evaluating this objective function can be extremely computationally expensive.

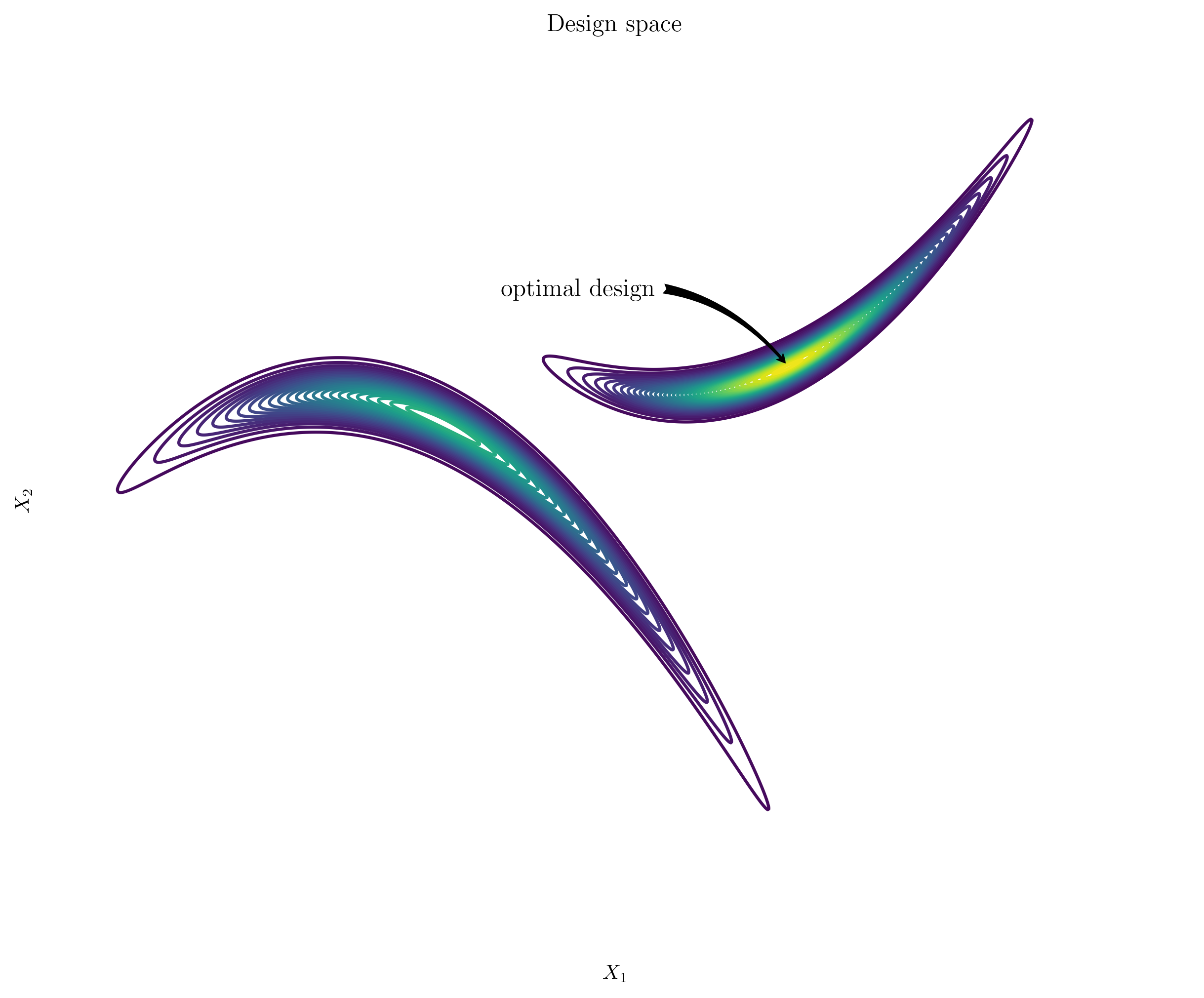
Grid search

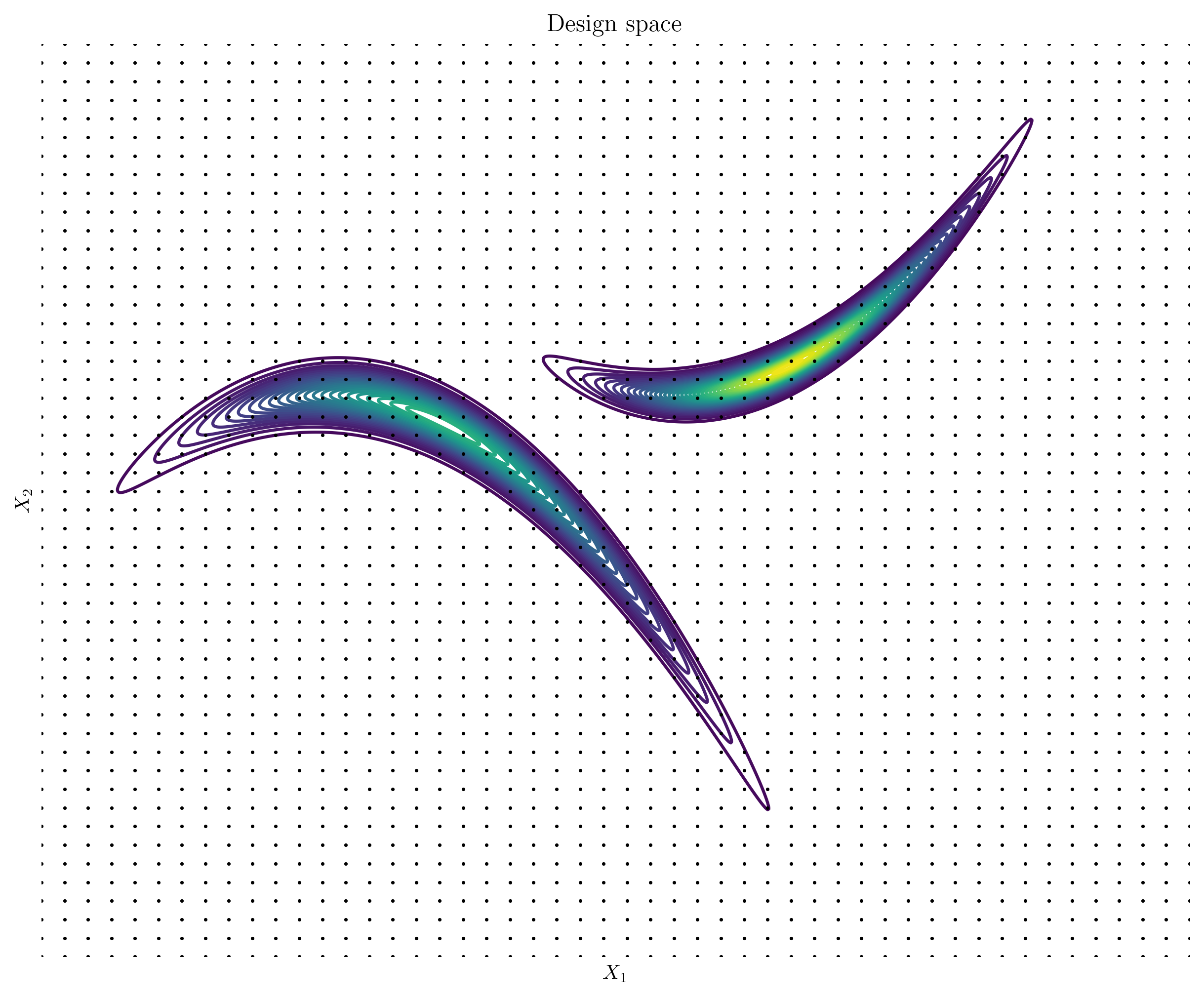
The simplest way to search the design space is through a grid search, where the space is divided into a uniform grid, and simulations are run at each grid point. While this method is straightforward and ensures systematic coverage, it suffers from the curse of dimensionality, where the number of required simulations grows exponentially with the number of dimensions. As a result, grid search becomes computationally impractical for problems with high-dimensional design spaces. In the following figure, each point represents a single run of a computationally expensive simulation.

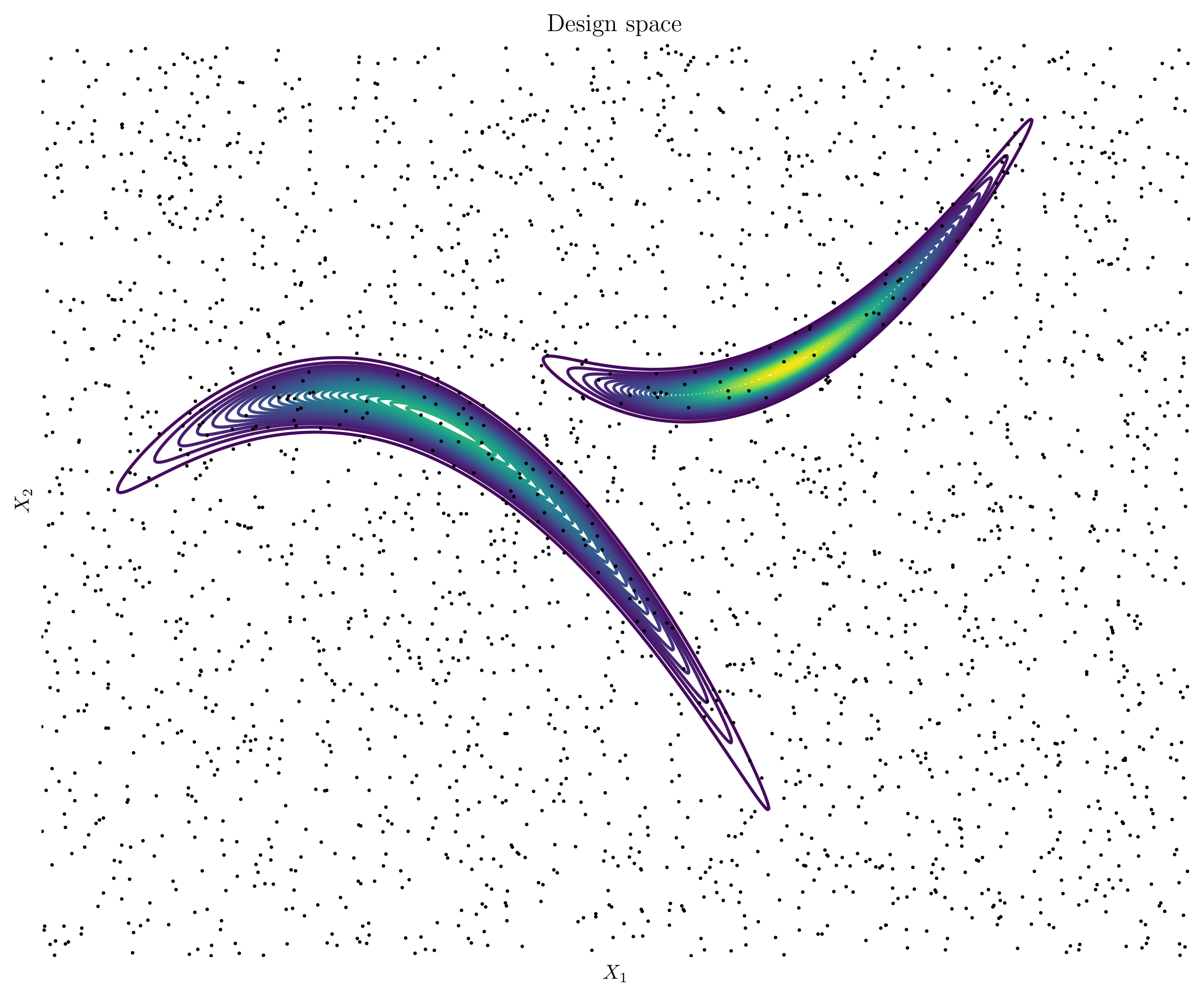
Monte Carlo (MC)

Monte Carlo sampling offers a more flexible approach to exploring the design space by randomly sampling points, avoiding the rigid structure of a grid. This method is less affected by the curse of dimensionality since the number of samples can be chosen independently of the dimensionality. However, it requires a large number of samples to achieve good coverage, especially in regions of interest. In the figure below, the randomly distributed points illustrate the stochastic nature of this approach.

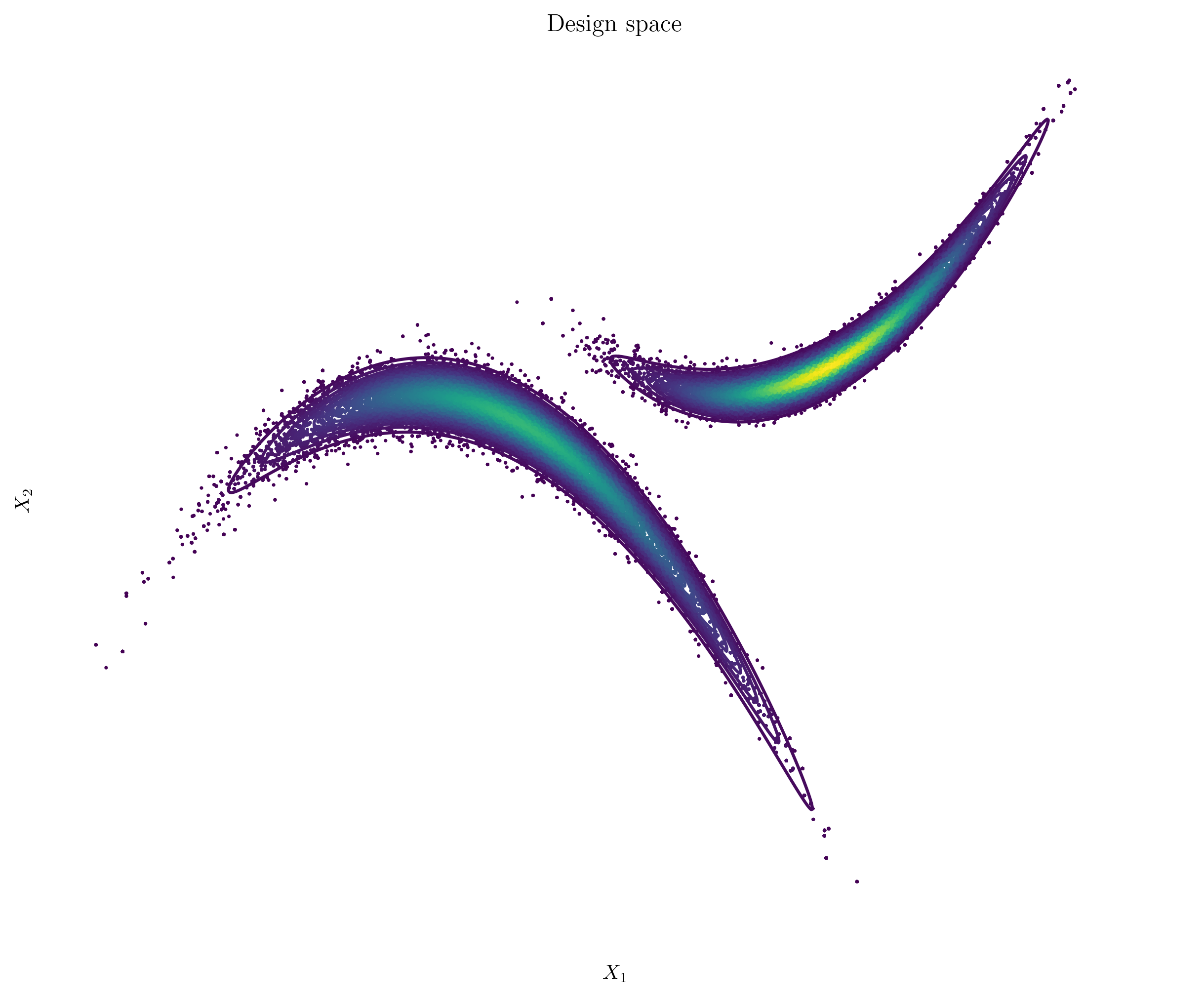
Markov Chain Monte Carlo (MCMC)

MCMC samplers systematically sample the design space in a way that favours regions with higher probability or likelihood, effectively focusing the exploration on the most probable designs. This approach is particularly useful when the goal is to understand the distribution of optimal solutions or identify regions of the design space that meet specific criteria, rather than exhaustively searching all possibilities.

Optimisation

The primary goal of optimisation is to find the best solution(s) according to specific objective criteria. The process inherently involves exploring the design space to identify regions that offer optimal performance. Techniques such as gradient-based optimisation, genetic algorithms, or Bayesian optimisation navigate the design space by sampling points, evaluating their performance, and iteratively refining the search. Thus, optimisation not only seeks the best designs but also contributes to understanding the structure and characteristics of the design space.

Gradient-based optimisation

Genetic algorithm